Đề Thi ĐGNL TP HCM 2025 Đợt 2 [Đề Chính Thức]

Tài liệu ôn thi chia sẻ Đề thi ĐGNL TP HCM 2025 chính thức đợt 2 dành cho các bạn ôn thi đánh giá năng lực HCM nhé. Đây là tài liệu sưu tầm các câu hỏi mà thí sinh nhớ được nên không đầy đủ và có thể có thiếu xót nhé.

Khi có update mới về đề thi chính thức ĐGNL TP HCM 2025 đợt 2, admin cũng sẽ update tiếp ở đây nhé. Các bạn có thể tham khảo Đề Thi ĐGNL TP HCM 2025 Đợt 1 chính thức

Nội dung bài viết

Đề Thi ĐGNL TP HCM 2025 Đợt 2

PHẦN III. TOÁN HỌC

Câu 61: Tìm $m$ để $(m+1)x^2 + 2(m+1)x + m + 3 > 0$ với $\forall x \in \mathbb{R}$ .
A. $m > -1$
B. $m > -\frac{3}{2}$
C. $m \ge -1$
D. $m \ge -\frac{3}{2}$

Câu 62: Cho hệ phương trình $\begin{cases} mx - y = m^2 \ x + (m-2)y = m-3 \end{cases}$ . Tìm $m$ để hệ phương trình có nghiệm duy nhất.
A. $0 < m$
B. $m \neq 1$
C. $m = 1$
D. $m \in \emptyset$

Câu 63: Số nghiệm của phương trình $\sqrt{2-2x} = \sqrt{1-x^2}$ là:
A. 2
B. 1
C. 0
D. 3

Câu 64: Cho $a, b$ thoả mãn $\log_b a = \log_b b = \log_a(2a+3b)-1$ . Gọi $S = \frac{a}{b}$ . Khẳng định đúng là:
A. $-1 < S < 0$
B. $2 < S < 3$
C. $0 < S < 1$
D. $1 < S < 2$

Câu 65: Cho $a > b > c > 1$ . Phương trình nào sau đây vô nghiệm?
A. $a^x + c^x = b^x$
B. $a^x + b^x + c^x = 1$
C. $a^x + b^x = c^x$
D. $b^x + c^x = a^x$

Câu 66: Tập xác định của hàm số $y = \frac{1}{\sqrt{4^x - 2}} + \ln(2x^2-4)$ là:
A. $(\sqrt{2}; +\infty)$
B. $\mathbb{R} \setminus { \frac{1}{2} }$
C. $\mathbb{R}$
D. $(\frac{1}{2}; +\infty)$

Câu 67: Số nghiệm thuộc $[0; 2\pi]$ của phương trình $\sin x \cos x (1+\tan x)(1+\cot x) = 1$ là:
A. 4
B. 1
C. 0
D. 3

Câu 68: Cho tam giác ABC có $\angle B = 60^\circ$ , $\angle C = 45^\circ$ , $AB=3$ . Tính AC.
A. $\sqrt{6}$
B. $\frac{2\sqrt{6}}{3}$
C. $\frac{3\sqrt{6}}{2}$
D. $\frac{3\sqrt{2}}{2}$

Câu 69: Cho tam giác ABC vuông tại A, BC = 24, AB = 12 thì $\cos C$ có giá trị là:
A. $\sqrt{3}$
B. $\frac{\sqrt{3}}{2}$
C. $\sqrt{2}$
D. $\frac{1}{2}$

Câu 70: Cho đồ thị hàm số $y = \frac{(2a-b)x^2 + ax + 2}{x^2 + ax + b - 6}$ nhận hai trục Ox, Oy làm hai tiệm cận. Giá trị $a+b$ là:
% Lưu ý: Câu này không có các lựa chọn A, B, C, D trong hình ảnh gốc.
% Nếu bạn có các lựa chọn, hãy thêm vào, hoặc đây là câu hỏi tự luận tìm giá trị. Đáp án tìm được là 9.

Câu 71: Giá trị của biểu thức $\lim_{h \to 0} \frac{\cos(x+h) - \cos x}{h}$ là:
A. $\cos(xh)$
B. $-\sin(xh)$
C. $-\sin x$
D. $\cos x$

Câu 72: Cho $f(x) = \frac{1-3x+x^2}{x-1}$ . Tập nghiệm của bất phương trình $f'(x) > 0$ là:
A. $\mathbb{R}$
B. $\emptyset$
C. $(1; +\infty)$
D. $\mathbb{R} \setminus {1}$

Cho A(5; -4; 2), B(1; 2; 4), C(1; 2; 1). Mặt phẳng (P) đi qua A và vuông góc với AB.

Câu 73: Phương trình mặt phẳng (P) là:
A. $2x - 3y - z + 8 = 0$
B. $2x - 3y - z - 20 = 0$
C. $3x - y + 3z - 13 = 0$
D. $3x - y + 3z - 25 = 0$

Câu 74: Khoảng cách từ C đến mặt phẳng (P) là:
A. $\frac{25\sqrt{14}}{14}$
B. $\frac{25}{14}$
C. $\frac{5}{14}$
D. $\frac{5\sqrt{14}}{14}$

Một phân xưởng có 2 máy M, N sản xuất 2 sản phẩm E, F. Một tấn E, F lãi lần lượt 2,2 triệu đồng và 1,8 triệu đồng. Muốn sản xuất E, máy M cần 3 giờ, máy N cần 1 giờ. Muốn sản xuất F, máy M cần 2 giờ, máy N cần 2 giờ. Biết 1 máy không thể sản xuất 2 sản phẩm cùng lúc. M hoạt động không quá 12 giờ, N hoạt động không quá 8 giờ trong một ngày. Gọi x, y là số tấn sản phẩm E, F sản xuất trong ngày.

Câu 75: Bất phương trình biểu diễn số giờ hoạt động của máy N trong 1 ngày là:
A. $x + y \le 6$
B. $x + y \le 4$
C. $3x + 2y \le 12$
D. $x + 2y \le 8$

Câu 76: Số tiền lãi lớn nhất có thể thu được trong 1 ngày là:
A. 9,8 triệu đồng
B. 10,2 triệu đồng
C. 8,8 triệu đồng
D. 10,6 triệu đồng

Cho cấp số cộng có $u_1 = 1$ , $S_{100} = 24850$ .

Câu 77: Công sai của cấp số cộng trên là:
A. 7
B. 10
C. 15
D. 5

Câu 78: Tính tổng: $M = \frac{1}{u_1 u_2} + \frac{1}{u_2 u_3} + \dots + \frac{1}{u_{49} u_{50}}$ .
A. $\frac{4}{23}$
B. $\frac{49}{246}$
C. $\frac{9}{246}$
D. 123

Cho hàm số $f(x) = x^3 - 9x^2 + 24x + m$ .

Câu 79: Tính $f'(1)$ .
A. $9+m$
B. $9$
C. $3$
D. $3+m$

Câu 80: Khi $m=3$ thì trung điểm I của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số có tọa độ là:
A. $(21;18)$
B. $(18;21)$
C. $(3;21)$
D. $(3;18)$

Câu 81: Tìm m để $f(x)=0$ có 3 nghiệm phân biệt
A. $-16 < m < 20$
B. $-20 < m < 16$
C. $-20 < m < -16$
D. $16 < m < 20$

Có hai hộp chứa thẻ. Hộp 1 chứa các thẻ đánh số thứ tự khác nhau từ 0 đến 100. Hộp 2 chứa các thẻ đánh số thứ tự khác nhau từ 0 đến 10.

Câu 82: Chọn ngẫu nhiên 2 thẻ từ hộp 1. Số cách chọn là:
A. 5050
B. 9900
C. 4590
D. 1000

Câu 83: Chọn ngẫu nhiên 2 thẻ từ hộp 2. Xác suất để 2 số thứ tự được chọn có tích là 1 số lẻ:
A. $\frac{2}{9}$
B. $\frac{2}{11}$
C. $\frac{3}{7}$
D. $\frac{3}{11}$

Câu 84: Chọn ngẫu nhiên từ mỗi hộp 1 thẻ. Xác suất để tổng 2 số thứ tự không vượt quá 90 là:
A. $\frac{82}{101}$
B. $\frac{59}{101}$
C. $\frac{25}{101}$
D. $\frac{86}{101}$

Cho tam giác ABC có phương trình (AB): $2x - y = 3$ , B(1; -1), C(6; 4).

Câu 85: Gọi I( $x_0$ ; $y_0$ ) là giao điểm của BC với Oy. Tính $x_0 + y_0$ .
A. 2
B. 0
C. 4
D. -2

Câu 86: Biết tam giác ABC vuông tại A. Tìm hoành độ điểm A.
A. 0
B. 4
C. 6
D. 2

Câu 87: Biết có 2 đường tròn đi qua C tiếp xúc đồng thời với Ox và Oy. Tổng bán kính của hai đường tròn này là:
A. 20
B. $8\sqrt{3}$
C. 16
D. $12\sqrt{2}$

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. $OA = \frac{\sqrt{2}}{2}$ , $OB = OC = 1$ .

Câu 88: Chu vi tam giác ABC là:
A. $\sqrt{2} + \sqrt{3} + \sqrt{6}$
B. $\sqrt{3} + \sqrt{6}$
C. $\sqrt{2} + \sqrt{3}$
D. $\sqrt{2} + \sqrt{6}$

Câu 89: Góc hợp bởi hai mặt phẳng (ABC) và (OBC) là:
A. $45^\circ$
B. $75^\circ$
C. $60^\circ$
D. $30^\circ$

Câu 90: Gọi H là hình chiếu vuông góc của O lên (ABC). Tính $V_{OABH}$ .
A. $\frac{\sqrt{2}}{48}$
B. $\frac{\sqrt{2}}{16}$
C. $\frac{\sqrt{2}}{24}$
D. $\frac{\sqrt{2}}{36}$

PHẦN IV. TƯ DUY KHOA HỌC

MỤC 3.1. LOGIC, PHÂN TÍCH SỐ LIỆU (Vé xe)

Một công ty có 3 tuyến xe 1, 2, 3 và in 3 bộ vé tháng 1, 3 bộ vé tháng 2. Mỗi tuyến sử dụng 1 bộ cho 1 tháng. Vé in theo quy tắc sau:
– Mỗi bộ 1 màu: xanh, đỏ, tím, vàng.
– Ở mỗi tuyến, vé tháng 1 khác màu vé tháng 2.
– Ở tuyến 3, vé tháng 1 hoặc vé tháng 2 có màu xanh.
– Ở mỗi tháng, vé cho các tuyến khác nhau thì có màu khác nhau.
– Một bộ vé ở tháng 1 có màu đỏ.
– Vé tháng 1 của tuyến 2 màu tím.
– Các vé tháng 2 không có màu tím.

Câu 91: Nếu vé tháng 1 của tuyến 3 có màu đỏ thì điều nào phải đúng?
A. Vé tuyến 3 của tháng 2 có màu xanh
B. Vé tuyến 1 của tháng 1 có màu vàng
C. Vé tuyến 1 của tháng 1 có màu xanh
D. Vé tuyến 2 của tháng 2 có màu vàng

Câu 92: Nếu 1 bộ vé (tuyến 2) có màu xanh thì điều nào phải đúng?
A. Vé tuyến 3 của tháng 2 có màu xanh
B. Vé tuyến 1 của tháng 1 có màu đỏ
C. Vé tuyến 1 của tháng 2 có màu đỏ
D. Vé tuyến 3 của tháng 1 có màu đỏ

Câu 93: Phát biểu nào có thể đúng?
A. Vé tháng 2 không có màu xanh
B. Chỉ có vé tuyến 2 màu đỏ
C. Tháng 1 có 1 bộ vé xanh, 1 bộ vé vàng
D. Vé tháng 1 không có màu xanh

MỤC LOGIC (Khách sạn)

Một dãy khách sạn đánh số thứ tự từ 1 đến 7 từ trái sang phải. Một đoàn khách có tên R, S, T, U, V, W, X sắp xếp ở 7 phòng (mỗi người 1 phòng). Phòng của T nằm bên trái phòng R; nếu S ở phòng 4 thì U ở phòng 5; nếu U ở phòng 6 thì S ở phòng 7; V và W không ở cạnh phòng nhau.

Câu 94: Liệt kê nào không thể là thứ tự phòng:
A. TRSUVXW
B. XSUVTRW
C. TXSUVRW
D. VUTSXRW

Câu 95: Nếu V và W ở phòng 5 và 7 thì 2 người nào không thể ở phòng 6?
A. ST
B. RS
C. XR
D. TU

Câu 96: T ở phòng 3, S ở phòng 4 thì phát biểu nào luôn đúng?
A. R ở trái V
B. X ở 1 hoặc 2
C. X, T cạnh nhau
D. W trái T

MỤC PHÂN TÍCH SỐ LIỆU (Điểm lớp)

Cho bảng điểm của 5 lớp. Nếu điểm thấp hơn 5 sẽ rớt môn, từ 5 điểm trở lên sẽ qua môn.

Lớp	<5	5-8	>8
1	28	72	24
2	15	68	36
3	18	52	28
4	29	58	47
5	30	60	35

Câu 97: Tổng số sinh viên của 5 lớp có bao nhiêu phần trăm rớt môn?
A. 18,8%
B. 20%
C. 15,6%
D. 21,2%

Câu 98: Trong số các sinh viên trên 8 điểm có 20\% sinh viên đạt điểm 10. Tỉ lệ sinh viên đạt điểm 10 của 5 lớp là:
A. 7,9%
B. 7,16%
C. 5,67%
D. 20%

Câu 99: Trong lớp mà tỉ lệ sinh viên rớt môn nhiều nhất, 1 số bạn đã phúc khảo và qua môn nên lớp đó không còn là lớp có tỉ lệ rớt môn nhiều nhất. Có ít nhất bao nhiêu bạn tăng điểm và qua môn sau khi phúc khảo?
A. 4
B. 1
C. 2
D. 3

MỤC PHÂN TÍCH SỐ LIỆU (Sách vở)

Số vở bán ra (đơn vị: nghìn cuốn) trong năm 2023 và 2024 của 6 công ty 1, 2, 3, 4, 5, 6 được thống kê như sau:

Công ty	Năm 2023	Năm 2024
1	80	105
2	75	65
3	95	110
4	85	95
5	75	95
6	70	80

Câu 100: Tổng số vở (nghìn cuốn) trong 2 năm của các công ty 1, 3, 5 là:
A. 250
B. 560
C. 310
D. 435

Câu 101: Tỉ lệ tổng số vở bán trong 2 năm của công ty 2 so với công ty 4 là:
A. 3:5
B. 7:9
C. 4:5
D. 2:3

Câu 102: Trong năm 2023, giá bán vở của công ty 5 và 6 như nhau. Trong năm 2024, công ty 5 tăng 10\%, công ty 6 tăng 15\% so với giá năm 2023. Tỉ lệ doanh thu công ty 5 với công ty 6 trong cả 2 năm là:
A. 113,5%
B. 88%
C. 110,8%
D. 90,3%

MỤC 3.1. SỐ LIỆU KHOA HỌC

(Áp suất hơi)

Áp suất hơi bão hoà của chất lỏng dễ bay hơi là áp suất hơi của nó khi tốc độ bay hơi bằng tốc độ ngưng tụ ở nhiệt độ xác định. Chất càng dễ bay hơi thì áp suất hơi bão hoà càng cao và khi nhiệt độ tăng thì áp suất hơi bão hoà tăng.

Khi hoà tan chất tan B (không bay hơi) vào dung môi A (dễ bay hơi) thì liên hệ giữa áp suất hơi bão hoà của dung dịch $P_A$ và áp suất hơi bão hoà của dung môi tinh khiết $P_A^0$ là

với $P_A^0 = 600 \text{ mmHg}$ .

Câu 103: Phát biểu nào sai:
A. Khi dung dịch hình thành, khả năng bay hơi của dung môi giảm
B. Khi nồng độ chất tan tăng thì áp suất hơi bão hoà tăng
C. Áp suất hơi bão hoà của dung môi tinh khiết luôn lớn hơn áp suất hơi bão hoà của dung dịch.

Câu 104: Cho $P_A = 400 \text{ mmHg}$ . Tính $\frac{n_B}{n_A}$ .
A. 1:2
B. 3:2
C. 2:3
D. 1:4

Câu 105: Cho $P_A = 200 \text{ mmHg}$ . Tính $\frac{n_B}{n_A}$ .
A. 5:2
B. 2:3
C. 3:2
D. 2:1

MỤC KHOA HỌC

(Thang nhiệt độ)

Hai thang nhiệt độ phổ biến là Celcius và Farentheit. Để xác định một thang nhiệt độ người ta cần xác định 2 mốc nhiệt độ làm chuẩn và chia thành các khoảng bằng nhau, mỗi khoảng ứng với một độ.

Thang Celcius: Điểm nóng chảy: $0^\circ \text{C}$ , điểm sôi: $100^\circ \text{C}$ của nước ở 1 atm. Chia thành 100 phần bằng nhau. Nhiệt độ của cơ thể con người bình thường là $37^\circ \text{C}$ .
Thang Farentheit: Điểm nóng chảy: $32^\circ \text{F}$ , điểm sôi: $212^\circ \text{F}$ của nước ở 1 atm. Chia thành 180 phần bằng nhau.

Câu 106: Công thức liên hệ đúng là:
A. $C = \frac{9}{5}F + 32$
B. $C = \frac{5}{9}F + 32$
C. $F = \frac{5}{9}C + 32$
D. $F = \frac{9}{5}C + 32$

Câu 107: Số chỉ của thang Celcius bằng với số chỉ thang Farenheit ứng với:
A. $-40^\circ \text{C}$
B. $4^\circ \text{C}$
C. $-4^\circ \text{C}$
D. $40^\circ \text{C}$

Câu 108: Chọn phát biểu đúng
A. Thân nhiệt người bình thường là $37^\circ \text{F}$ .
B. $32^\circ \text{F}$ là nhiệt độ nước đá đang tan ở 1 atm.
C. Trong thang Farentheit, từ điểm nóng chảy đến điểm sôi, chia thành 100 phần bằng nhau, mỗi phần ứng với 1 độ.
D. $100^\circ \text{C}$ là nhiệt độ độ sôi của nước ở 1,5 atm.

MỤC KHOA HỌC (Thí nghiệm Sinh học – Bèo)

Nhằm đánh giá khả năng sinh sản của bèo, tiến hành thí nghiệm ở nhiệt độ phòng, mỗi đĩa có 3 cây bèo nuôi ở 4 môi trường: (1) nước cất, (2) nước ao, (3) dung dịch NPK, (4) dung dịch giàu nitrat. Cho biểu đồ sau:

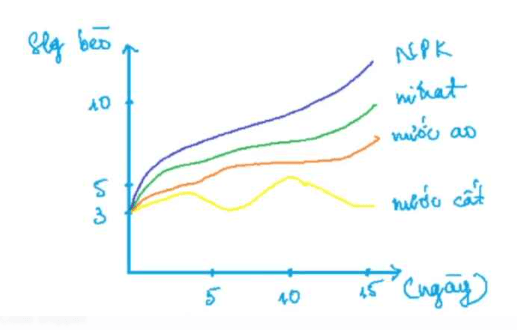
Câu 109: Sau 10 ngày thì ở nước cất có bao nhiêu bèo tấm?
A. 2-3
B. 5-6
C. 9-10
D. 3-4

Câu 110: Bèo sinh sản nhanh nhất ở môi trường nào?
A. Nước ao
B. Nước cất
C. Dung dịch NPK
D. Dung dịch nitrat

Câu 111: Từ kết quả thí nghiệm, cho các nhận định:
(I): Sau thời gian nuôi trong nước cất, bèo bị chết.
(II): Môi trường giàu nitrat tạo thuận lợi cho nuôi bèo.
(III): Nước ao chứa chất ức chế cho bèo.
(IV): Thiếu các khoáng chất NPK làm bèo chết.

Các nhận định đúng là:
A. I, II
B. I, III
C. II, III, IV
D. II, IV